When can we say one computer / architecture / design is better than others?
- Desktop PC (execution time of a program)
- Server (transactions / unit time)
When can we say X is n times fasterthanY ?
- Execution time(y) / Execution time(x) =n
- Throughput(x) / Throughput(y) = n
Typical performance metrics
- Response time - When a request is coming from a machine to another machine, the time for the second machine to respond to that request is known as response time
- Throughput - Number of task that is completed in a unit time
- CPU time - Total time associated with respect to a program in cpu execution
- Wall clock time - Actual time taken for a program to execute ie sum total of cpu time and non-cpu time(peripheral time)
- Speedup - If the execution time of one is larger than other then it means speedup
Benchmarks
- Toy programs (e.g. sorting, matrix multiply)
- Synthetic benchmarks (e.g. Dhrystone)
- Benchmark suites (e.g. SPEC06, SPLASH)
SPECRatio
SPECRatio(A) = Execution time(reference) / Execution time(A)
Reference for SPEC 2006: Sun Ultra Enterprise 2 workstation with a 296-MHz UltraSPARC II processor
Amdhal's Law
- Amdahl’s Law defines the speedup that can be gained by improving some portion of a computer.
- The performance improvement to be gained from using some faster mode of execution is limited by the fraction of the time the faster mode can be used.
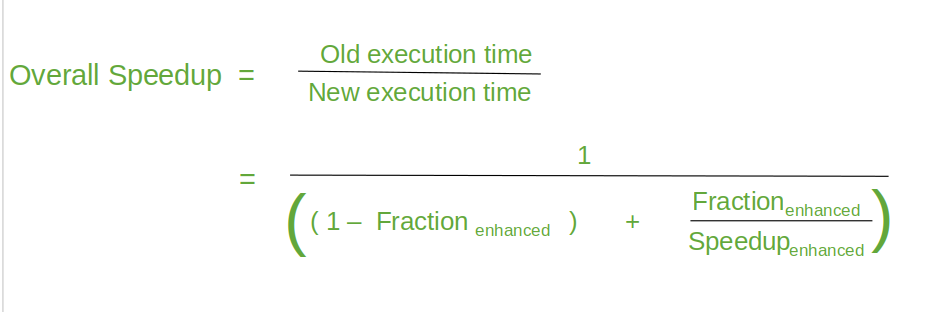
Example
Suppose that we want to enhance the floating point operations of a processor by introducing a new advanced FPU unit. Let the new FPU is 10 times faster on floating point computations than the original processor. Assuming a program has 40% floating point operations, what is the overall speedup gained by incorporating the enhancement?
Solution:
- Fraction enhanced = 0.4
- Speedup enhanced = 10
- Therefore speedup = 1/(0.6 + 0.4/10) = 1.56 times faster
Example
A common transformation required in graphics processors is square root. Implementations of floating-point (FP) square root vary significantly in performance, especially among processors designed for graphics. Suppose FP square root (FPSQR) is responsible for 20% of the execution time of a critical graphics benchmark.
One proposal is to enhance the FPSQR hardware and speed up this operation by a factor of 10. The other alternative is just to try to make all FP instructions in the graphics processor run faster by a factor of 1.6; FP instructions are responsible for half of the execution time for the application. Compare these two design alternatives using Amdahl's Law.
Solution:
- Case A: FPSQR hardware optimization
- S = 1.219
- Case B: FP instructions optimization
- S = 1.23
Principles of Computer Design
- All processors are driven by clock.
- Expressed as clock rate in GHz or clock period in ns
- CPU Time = CPU clock cycles x clock cycle time
CPl = CPU clock cycles for a program / Instruction Count CPU Time = IC * CPI * CCT
- Clock cycle time- hardware technology
- CPI- Organization and ISA
- IC-ISA and compiler technology
Example: Basic Performance Analysis
Consider two programs A and B that solves a given problem. A is scheduled to run on a processor P1 operating at 1 GHz and B is scheduled to run on processor P2 running at 1.4 GHz. A has total 10000 instructions, out of which 20% are branch instructions, 40% load store instructions and rest are ALU instructions. B is composed of 25% branch instructions. The number of load store instructions in B is twice the count of ALU instructions. Total instruction count of B is 12000. In both P1 and P2 branch instructions have an average CPI of 5 and ALU instructions has an average CPI of 1.5. Both the architectures differ in the CPI of load-store instruction. They are 2 and 3 for P1 and P2, respectively. Which mapping (A on P1 or B on P2) solves the problem faster, and by how much?

Amdahl's Law
A company is releasing 2 latest versions (beta and gamma) of its basic processor architecture named alpha. Beta and gamma are designed by making modifications on three major components (X, Y and Z) of the alpha. It was observed that for a program A the fractions of the total execution time on these three components, X, Y, and Z are 40%, 30%, and 20%, respectively. Beta speeds up X and Z by 2 times but slows down Y by 1.3 times, where as gamma speeds up X, Y and Z by 1.2, 1.3 and 1.4 times, respectively. a. How much faster is gamma over alpha for running A? b. Whether beta or gamma is faster for running A? Find the speedup factor
Solution: a. Gamma is 1.239 times faster over alpha b. Beta is faster than gamma -> 1.267/1.239 = 1.022 times